时间复杂度和空间复杂度

发表于 | 分类于 |

这一节学的主要是时间复杂度和空间复杂度。

时间复杂度

定义

如果给每一句代码执行的时间定义为 unit_time，那么执行 n 次所需要的代码执行时间，则是 T(n) = unit_time * n。所以，可以看出，执行时间与执行次数是一个正比的关系。那么将其总结成一个公式，则是我们熟知的大O。

1

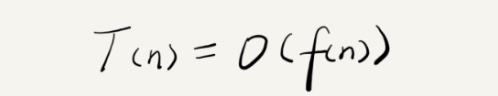
方法

对于分析时间复杂度的方法，可以关注三个。

  1. 只关注循环执行次数最多的一段代码
  2. 加法法则：总复杂度等于量级最大的那段代码的复杂度
  3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常见的一些复杂度分析

常见的时间复杂度有：常数阶 𝙊(1)，对数阶 𝙊(logn)，线性阶 𝙊(n)，线性对数阶 𝙊(nlogn)，平方阶 𝙊(n^2)，立方阶 𝙊(n^3)，…， k次方阶 𝙊(n^k)，指数阶 𝙊(2^n) 等。

  • 𝙊(1)

    常数级别的时间复杂度。比如一句简单的代码，甚至是几句代码。只要代码的执行时间不随着 n 的增大而增长的，那么其时间复杂度都可以是 𝙊(1)

  • 𝙊(n)

    这个时间复杂度也是比较常见的。经常是简单代码循环 n 次的话，基本就是 𝙊(n) 的时间复杂度。比如

    1
    2
    3
    4
    int i = 0, sum = 0;
    for (; i <= n; i++) {
        sum += i;
    }

  • 𝙊(log n)

    其实是从等比数列的求和公式推导出来的。

    1
    2
    3
    4
    i=1;
    while (i <= n)  {
      i = i * 2;
    }
按照上述的代码，如果要算得代码总的执行时间，那么则是`2^0 + 2^1 + 2^2 + 2^x >= n`。左边的式子，其实就是等比数列的求和。那么根据求和公式，可以得到这样的关系: 
`2^0 * (1 - 2^x) / (1 - 2) >= n`。

那么简化得到的式子其实是`2^x - 1 >= n`，因为 n 无限大时，n + 1 和 n 其实没啥区别。因此再简化，则是`2^x = n`。因为时间复杂度涉及到的是 x 的次数，所以上述代码的时间复杂度其实就是`𝙊(log2(n))` 。那么如果是底数为 3 的话，则是 log3(n) 了。根据对数的乘法法则，log3(n) 其实就等同与 log3(2) * log2(n) 。很显然，log3(2) 是一个常数，那么在计算 𝙊 时，可以进行忽略，也就是 𝙊（log3(n)） 等于 𝙊（log2(n)）。那么忽略对数的底，就可以得到一个较为统一的表达式，也就是 𝙊（logn）。

  • 𝙊(nlogn)

    其实，𝙊(nlogn) 就相当于 𝙊(log n) 循环 n 次得到的结果。比如一个简单例子，在 𝙊(log n) 中的例子中，再套上个循环。

    1
    2
    3
    4
    5
    6
    7
    int j = 0;
    for (; j <= n; j++) {
        int i = 1;
        while (i <= n)  {
            i = i * 2;
        }
    }

  • 𝙊(n^2)

    这个时间复杂度其实就是多重嵌套循环。一个简单的🌰。

    1
    2
    3
    4
    5
    6
    7
    int j = 0, sum = 0;
    for (; j <= n; j++) {
        int i = 0;
        for (; i <= n; i++)  {
            sum += i;
        }
    }

    总的执行时间其实就是
    T(n) = (1 1 + 1 2 … + 1 n) + (2 1 + … + 2 n) + … + (n 1 + … + n * n)

    那么，很显然就是 T(n) = 𝙊(n^2) 。从这里也可以得知时间复杂度的一个特性，取最高的幂次数。

    当然也能得到其他类似的时间复杂度。比如 n^3, n^4 。。。

  • 𝙊(2^n)

    暂时还没想到对应的。

  • 𝙊(n!)

    暂时还没想到对应的。

  • 𝙊(m + n)

    这种复杂度其实可以看成是两个数据规模 m 和 n ，由于无法实现评估两个量级谁大，所以无法忽略。因此才会是 𝙊(m + n)。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    int sum_1 = 0;
    int i = 1;
    for (; i < m; ++i) {
        sum_1 = sum_1 + i;
    }
    int sum_2 = 0;
    int j = 1;
    for (; j < n; ++j) {
        sum_2 = sum_2 + j;
    }

  • 𝙊(m * n)

    按照上述的例子，其实就是两重循环嵌套这样，从而得到 𝙊(m * n) 这样的时间复杂度

    1
    2
    3
    4
    5
    for(int i = 1; i < m; i++) {
        for(int j = 1; j < n; j++) {
            ....
        }
    }

最好、最坏情况时间复杂度

有时候，代码在不同情况下的不同时间复杂度，也会有所差异。因此，才有了一些概念：最好情况时间复杂度、最坏情况时间复杂度、平均情况时间复杂度。

1
2
3
4
5
6
7
8
9
10
11
12
// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
       pos = i;
       break;
    }
  }
  return pos;
}

像这个🌰，最好情况时间复杂度即是我们遍历到第一个元素都匹配到了，那么此时的时间复杂度应该是 𝙊(1)。而最坏情况时间复杂度即是我们遍历到最后一个元素才匹配到，那么此时的时间复杂度应该是 𝙊(n)。
那么平均情况时间复杂度呢？

前两者均是极端情况下才发生的。而平均情况时间复杂度则需要引入概率论。假设在数组中与不在数组中的概率都为 1/2 ，而要查找的数据出现在 0～n-1 这个 n 个位置的概率都是一样的 1/n 。那么要查找的出现在数组中的任意位置的概率就是 1/(2n) 了。

因此，平均情况时间复杂度则是需要把各种情况考虑进去。

2

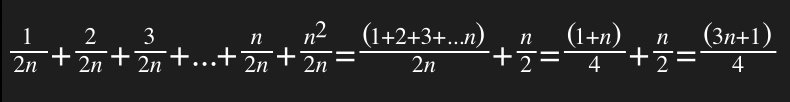
大致上可以得到这样的情况，利用加权平均值得到平均情况时间复杂度。而根据时间复杂度可以进行忽略常数项等，那么平均情况时间复杂度则是𝙊(n)。

均摊时间复杂度

直接上🌰吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// array 表示一个长度为 n 的数组
// 代码中的 array.length 就等于 n
int[] array = new int[n];
int count = 0;
void insert(int val) {
   if (count == array.length) {
      int sum = 0;
      for (int i = 0; i < array.length; ++i) {
         sum = sum + array[i];
      }
      array[0] = sum;
      count = 1;
   }
   array[count] = val;
   ++count;
}

均摊时间复杂度其实算是一种特殊的平均时间复杂度。比方说上述的例子，大多数情况下的时间复杂度是𝙊(1)，只有等到 count 等于数组长度时，时间复杂度才会是𝙊(n)。不同于平均时间复杂度有着一些极端情况，而上述例子却只有在个别情况下才会是𝙊(n)。按照上述的例子，每一次进行一个𝙊(n)的操作后，接下来的 (n-1)次均会是𝙊(1)的操作。因此可以𝙊(n)均摊下来，可以得到𝙊(1)的均摊时间复杂度。

空间复杂度

空间复杂度，其实就是算法的存储空间与数据规模之间的增长关系。比如，生成一个变量，则是占据了 1 个存储单位。同比与时间复杂度，一段代码中，常数级别的复杂度可以忽略不计，只关注量级最大的相关代码。具体计算和时间复杂度相当。

1
2
3
4
5
6
7
8
9
10
11
void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }
  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

int i = 0生成 1 个存储单位，而第一个循环中，给数组 a 中赋值 i，则相当于不停地生成存储单位，那么则是 n 个存储单位。因此是整个方法的空间复杂度即是 𝙊(n)。和时间复杂度类似，也有其他的一些相同的复杂度，比如 𝙊(1)，𝙊(logn)等。

总结

时间复杂度和空间复杂度是用来衡量一些效率问题的，比如说一个算法的优劣。但是我觉得平时在工作上能用的情况有点少。比方说消息列表去检索数据等？目前想到的是这些。